2020. 5. 21. 14:09ㆍ통계 빠개기/Statistics
Chi-Square(카이제곱) 분포는 무엇이고, 카이제곱 통계량은 어떻게 도출되었을까?
통상 학부 통계학 수업의 '연속확률분포' 부분에서 처음 접하게 되는 Chi-square 분포. 이 역시 정규분포...
blog.naver.com
Chi-Square(카이제곱) 분포는 무엇이고, 카이제곱 통계량은 어떻게 도출되었을까?
Normal : The Kevin Bacon of Distributions (정규분포 : 확률분포의 케빈 베이컨)
정규분포의 중요성에 대해서는 지난 포스트에서 살펴보았다. 그러면서 Minitab Blog의 글을 따라 정규분...
blog.naver.com
향후 회귀분석/분산분석을 이해하려면 F분포를 알아야하는데, 이 F분포는 또 Chi-Square 분포와 깊은 관련이 있다. 그리고 Chi-Square 분포는 그 자체로 카이제곱 검증 등에서 쓰이기도 한다. 그래서 이번 포스트에서는 먼저 이 Chi-Square 분포가 무엇이고, 누가 왜 만들었으며, 이는 어디에서 주로 활용되는지에 대해 알고 넘어가도록 하자.
□ Chi-Square 분포의 정의
간단히 말하면, Chi-Square 분포는 '표준정규분포 확률변수의 제곱합'으로 정의된다.
이를 더 풀어보면, Z1..Zn이 n개의 상호 독립인 확률변수로서 각각 평균이 0이고 분산이 1인 표준정규분포를 따를 때, 이 Zi들을 제곱하여 합한 값으로 정의되는 새로운 확률변수(X)는 자유도가 n인 Chi-Square 분포를 따른다고 한다는 것.
이를 X = ∑ (Zi²) ~ χ²(n) 이라고 표현한다.
그리고 (당연하겠지만) X~N(u,σ)일 때, Z = (X-u) / σ는 N(0,1)을 따르고, 이 표준정규변수 Z를 제곱한 Z² = (X-u)² / σ²는 자유도가 1인 χ²(1)를 따르게 된다. 즉, Z² ~ χ²(1)
□ Chi-Square 분포의 주요 특성
1) 앞서 나온 정규분포, t분포와는 다르게, 좌우 대칭의 종형이 아니다.
2) 단, n의 크기가 증가하게 되면 점점 대칭성을 갖추게 되어, 통상 n이 30 이상이면 거의 정규분포에 가까워진다.
3) 그리고, 분포의 정의에서 봤듯이 제곱하여 합한 개념이므로, 0보다 큰 영역에서만 그려진다.
4) 마지막으로, X가 χ²(n1) 분포를 하고, Y가 χ²(n2)의 분포를 할 경우, X와 Y가 확률적으로 서로 독립이라면, X+Y는 χ²(n1+n2)가 된다. 이를 'χ² 분포의 가법성'이라고 한다.
□ 누가, 왜 Chi-Square 분포를 만들었나?
국내외 통계학 원론 교재들을 보면, t분포는 소개할 때 맥주회사인 기네스 이야기가 나오기도 하고 Student라는 t분포를 만든 Gosset의 필명이 나오기도 하는데, 카이제곱 분포를 누가 만들었는지에 대한 설명이 나오는 교재는 아직 보지 못한 것 같다.
Wikipedia를 찾아보면, Chi-Square 분포는 영국의 통계학자인 Karl Pearson이 1895년에서 1916년 경까지 개발한 일련의 연속확률분포 중의 한 가지라고 나온다. Pearson은 연속적인 두 변수간의 상관계수인 Pearson's Correlation으로 유명한데, 사실 그는 University College London에 1991년 세계 최초의 통계학과를 세웠을 뿐만 아니라 Gosset 보다 먼저 t 분포를 확인했다고.
* Pearson's 1895 paper introduced the type IV distribution, which contains Student's t-distribution as a special case, predating William Sealy Gosset's subsequent use by several years. (Wikipedia, "Pearson Distribution" 中)
□ Chi-Square 분포는 언제 쓰이는가?
1) 표본분산 s²의 분포
통계학 교과서에서 Chi-Square 분포가 처음 활용되는 부분은 표본분산 s²의 분포가 나오는 곳인 것 같다. 모분산 σ²의 불편추정량이 s²임을 설명하며 (n-1) * s² / σ²는 χ²(n-1)의 분포를 따른다는 부분인데, 통상적으로 '수리통계학 교재에서 다루는 내용', '이 책의 수준을 넘으므로'라고 하며 은근슬적 넘어가는 경우가 많다. 근데 사실 이는 분포의 정의와 Chi-square 분포의 4번째 성질을 생각하면 쉽게 구해지는 결과이며, 이는 결국 표본표준편차를 구할 때 n이 아닌 n-1로 나누는 이유이기도 하다. 그리고 이를 활용해 모집단 분산에 대한 가설검정을 한다.
2) 범주형 자료 분석의 카이제곱 검정
Chi-Square 분포는 어떤 확률변수가 특정 분포를 따른다는 적합도 검정과, 두 변수간의 통계적 독립성을 검정하는 데에도 활용된다. 두 가지 경우 모두 관측빈도와 기대빈도를 가지고 만들어지는 카이제곱 통계량을 활용하며, 적합도 검정은 변수가 1개 일때, 독립성 검정은 변수가 2개 일 때 쓰인다는 차이가 있다.
이 때 활용되는 카이제곱 통계량은 다음과 같이 정의되며, 기대빈도수인 Ei가 모두 5 이상인 조건을 만족하면 귀무가설이 참이라는 가정하에서 근사적으로 χ²(n-1)을 따르는 것으로 알려져 있다고 한다.

* Oi는 관측빈도수
Ei는 기대빈도수
왜 이 통계랑이 χ² 분포를 따르는지에 대해서는 통계학 원론 책에는 거의 설명이 나오지 않는다. 한 군데 겨우 찾은 것이 '기초통계학의 숨은 원리 이해하기'의 저자인 김권현 님의 블로그. 김권현 님에 따르면, 이 유도 방법을 설명해주는 통계학 책은 거의 없다고 하며, 본인의 책에서도 이 내용은 제외되어 있다. 블로그에만 있는건데, '수식이 지나치게 많아서' 인듯..
https://math100.tistory.com/45
카이제곱분포표 보는 법
카이제곱분포는 t분포와 마찬가지로 확률을 구할 때 사용하는 분포가 아니라, 나중에 신뢰구간이랑 가설검정에서 사용하는 분포다. 그래서 카이제곱분포표는 “t분포표 보는 법”과 얼추 비슷�
math100.tistory.com
http://blog.daum.net/gongdjn/117
[12-3] 카이제곱 분포 chi-square distribution 와 정규분포 normal distribution
※ 자료 출처 : Mathematical statistics with applications (K. M. Ramachandran, C.P. Tsokos 저) 1. 왜 카이제곱 분포가 필요한가? 앞 장에서는 주로 표본들의 평균에 해당하는 통계량 에 대해서 알아보았다...
blog.daum.net
http://blog.daum.net/gongdjn/117
※ 자료 출처 : Mathematical statistics with applications (K. M. Ramachandran, C.P. Tsokos 저)
1. 왜 카이제곱 분포가 필요한가?
앞 장에서는 주로 표본들의 평균에 해당하는 통계량

에 대해서 알아보았다.
카이제곱 분포를 본격적으로 공부하기 전에 잠깐 정리를 해보자.
1) 모집단 → 무작위 표본 추출
2) 무작위로 추출된 표본을 각각 다음과 같이 확률 변수로 보자.
3) 추출된 표본으로 계산할 수 있는 통계량을 다음과 같이 정의한다.

4) 위에서 정의된

는 다음과 같이 중요한 성질을 갖는다.
- 모집단의 확률 분포는 모르지만 평균(

)과 분산(

)을 알고 있을 때,


- 만약

일 때,

를 다음과 같이 정규화해주면


- 모집단이 다음과 같이 정규 분포를 가진다고 알려져 있을 때,


는 다음과 같은 분포를 따른다.
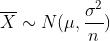
만약

를 표준화해주면,

이제 다음과 같이 질문을 던져보자. 과연

의 분포를 안다는 것이 어떤 의미가 있는가?
우리는 앞에서 예제 문제를 풀면서 이에 대해서 잠깐 살펴봤다.
앞에서 풀었던 예제 문제를 다시한번 살펴보도록 하자.
바로 전 장의 예제에서 자동차 회사의 주장은 다음과 같았다.
우리 차의 연비는 평균 리터당 18km이며 표준편차 2의 정규 분포를 이룬다.
자동차 회사의 주장이 사실인지 증명하기 위해서
무작위로 자동차 16대 ()를 골라서 그 연비를 측정했다.
이때 각각 측정된 연비는 다음과 같이 정의된 확률 변수의 값이라고 할 수 있다.
한편 이 확률 변수들의 평균을 통계량
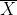
라고 정의하자.
이 예제에서는 딱 한번 측정을 했지만,
실제로는 똑같은 측정을 여러번 해준다는 전제가 깔려 있다.
예를 들어, 다음 표를 보자.

만약 회사의 주장이 사실이라면

는

이어야 한다.
자, 이제 실제 측정 데이터로 돌아오자.
실제로는 위와 같이 여러번 측정해준 것이 아니라 딱 한번 측정을 해주었고, 그 때

라는 값이 나왔다.
이제 우리는

의 분포로부터
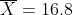
아라는 값이 나오기가 쉬운 지 어려운 지 판단하여
회사의 말이 진실인지 거짓인지 판단할 수 있다.
여기까지 우리는

라는 통계량만을 살펴봤지만,
실제 누군가의 관심사는

가 아닐 수도 있다.
즉, 위 예제에서 검증하고자 하는 것은 회사가 주장하는 리터당 18km였지만,
어떤 사람은 그것보다 표준편차 2km/liter를 검증해보고 싶을 수도 있다.
이런 경우 우리는 또다른 통계량 을 계산해야 한다.
은 다음과 같이 정의된다.
무작위로 추출된 표본 확률 변수가 다음과 같이 주어져있다고 가정해보자.
이 때,

의 기대값은 다음과 같이 계산할 수 있다.
을 다음과 같이 살짝 변형해보자.

따라서,

한편,

와

에 대하여 다음과 같은 식이 성립해야 한다.

또한,

이므로


따라서,

앞의 자동차 연비 구하는 문제에서 만약 회사에서 주장하는 표준편차를 검증하고 싶다면
통계량

와 더불어 도 함께 구해야 한다.
예를 들어 보면,

와 같이 을 함께 구하면 그 평균은 모평균의 분산값으로 수렴해야만 한다.
하지만 위의 예제처럼 실제 실험은 여러번 수행되는 것이 아니라
딱 한번 수행되며, 그 때 얻어진 통계량 의 값이 타당한가를 판단하여
회사에서 주장하는 주장이 맞는지 확인할 수 있다.
이 때, 에 대한 판단을 위해서는
사전에 이 어떤 분포 함수를 따르는지 알아야만 한다.
우리가 이제부터 배울 카이제곱 분포는 의 분포와 밀접한 관련이 있다.
2. 카이제곱 분포
카이제곱 분포는 감마 분포의 특별한 경우이다.
(감마 분포 함수에 대해서는 여기를 참조.)
즉,

여기서 n이 양의 정수일 때, 자유도 혹은 degree of freedom(d.f)라고 부른다.
카이제곱 분포를 따르는 확률 변수의 확률 밀도 함수를 여기서 다시 써보자.

그리고 카이제곱 분포를 따르는 확률변수의 평균, 분산 및 mgf는 다음과 같다.

눈여겨 볼 부분은 카이제곱 분포를 따르는 확률 변수는 그 평균이
자유도와 같다는 점이다.
자, 이제 카이제곱 분포를 따르는 확률 변수의 몇가지 특징을 알아보도록 하자.
카이제곱 분포를 따르고 서로 독립적으로 각각 자유도가 인
확률 변수를 다음과 같이 적어보자.
이 때, 이 확률 변수들의 합으로 정의되는 확률 변수를 다음과 같이 정의해보자.
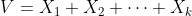
새롭게 정의된 확률 변수

는 자유도가

인 카이제곱 분포를 따른다.
위 성질은 mgf의 다음 특성을 이용하면 쉽게 증명이 가능하다.
와

가 서로 독립적일 때,

즉,

위 식은
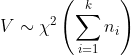
임을 암시한다.
한편, 카이제곱 분포가 굉장히 중요한 이유는 정규 분포와 밀접한 관계를 가지고 있기 때문이다.
일단 표준 정규 분포와 카이제곱 분포의 관계는 다음과 같이 쓸 수 있다.
확률 변수 가 표준 정규 분포를 따른다고 가정해보자.
이 때,

은 자유도 1의 카이제곱 분포를 따른다.
이 증명은 두가지 방법으로 할 수 있는데,
1) Method of distribution functions 으로 하는 증명하는 방법은 이미 다룬 바가 있다. (여기 참조)
2) mgf를 이용하는 방법
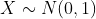
일 때, mgf는 다음과 같이 쓸 수 있다.

따라서

(위 적분은 직교좌표계에서 극좌표계로 좌표계를 변환하면 할 수 있다.)
위 식과 원래 카이제곱 분포의 mgf를 비교하면,
위 식은 n=1일 때라는 것을 알 수 있다.
즉,
위에서 살펴본 두가지 성질을 이용하면 다음을 증명할 수 있다.
평균이

이고 분산이

인 정규분포를 따르는 모집단이 있다고 가정해보자.
이 모집단으로부터 개의 표본을 무작위로 추출했을 때 각각의 표본을 다음과 같이 확률 변수로 정의하자.
이 확률 변수들에 대해서 각각을 표준 정규화해준 뒤, 제곱을 하여, 모두 더해보자.
즉,
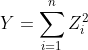
이 때,
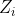
는 모두 독립적으로 표준 정규 분포를 따른다.
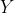
는 자유도 의 카이제곱 분포를 따른다.
카이제곱 분포는 보통 카이제곱표의 형태로 주어진다.
카이제곱 표를 보는 방법에 대해서 잠깐 알아보자.
만약 카이제곱 분포를 따르는 어떤 확률 변수가 다음과 같이 주어져있다고 가정해보자.

카이제곱 표를 이용하여 다음의 값을 찾을 수 있다.

카이제곱 분포를 이용하는 예를 들어보자.
을 따른다고 알려진 모집단으로부터 추출된 표본 확률 변수 5개를 다음과 같이 써보자.
이 때 다음을 만족하는

값을 구하여라.
확률 변수를 다음과 같이 정의해보자.


는 자유도 5의 카이제곱 분포를 따른다.
따라서 우리가 구하고자 하는

값은 다음을 만족해야 한다.

이것은 곧 다음과 같이 다시 쓸 수 있다.

자유도 5의 카이제곱 테이블은 다음과 같이 주어진다.
위 표로부터 a값은 9.24이다.
이 글의 도입부에서 처음 설명했지만,
카이제곱 분포가 중요한 이유는 통계량 의 분포에 대한 단서를 제공하기 때문이다.
실제 의 분포와 카이제곱 분포의 관계를 다음 정리를 통해 살펴보도록 하자.
평균이

이고 분산이

인 정규 분포를 따르는 모집단으로부터 추출된 개의 표본 확률 변수가 다음과 같이 주어져있다.
이 때 다음과 같은 확률 변수를 정의하면,

이 확률 변수는 자유도

의 카이제곱 분포를 따른다.
위 정리를 증명해보자.
우리는 앞에서 위에서 주어진 에 대해서
다음이 성립함을 이미 살펴보았다.

자 이제 위 식을 다음과 같이 변형해보자.
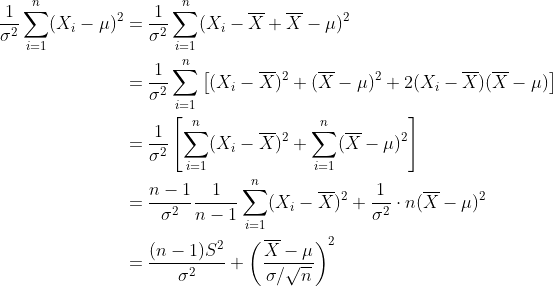
위 식의 중간에

한편 위 식을 잘 보면,
이 된다는 것을 알 수 있다.
따라서 카이제곱 분포의 성질에 따라서
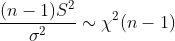
우리는 이 정리를 모집단의 분산값에 대한 추론이나 검증 등에 사용할 수 있다.
이미 살펴보았지만 통계량 의 기대값은 모집단의 분산값이 되는데,
만약 우리가 어떤 조사를 통해서 구해낸 값이 타당한가에 대한 판단은
의 샘플링 분포에 전적으로 의존하게 된다.
다음 예제를 통해서 좀더 자세히 살펴보자.

으로 알려진 정규분포로부터 표본 확률 변수를 무작위로 다음과 같이 추출하였다.
다음을 만족하는 양수

와

를 구하여라.

다음이 성립하므로

한편 위 식을 만족하는 값은 a와 b값은 무한히 많다.
하지만 카이제곱표를 통해서 가장 쉽게 찾을 수 있는 방법은
카이제곱 분포에서 아래쪽 0.05, 위쪽 0.05를 잘라내는 것이다.
따라서 무수히 많은 a, b 중에 다음 a, b값은 원래 식을 만족한다.

즉,

을 만족한다.
우리는 이 문제로부터 다음과 같은 추론을 할 수가 있다.
만약, 모집단으로부터 9개의 표본을 추출해서 을 계산해봤더니,
0.273과 1.551을 벗어나는 값이 나왔다면?
의 분포 함수를 고려했을 때 이것은 굉장히 예외적인 경우로서
측정이 잘못되었거나 원래 모집단의 분산으로 알려진 값이 틀릴 가능성이 높다.
이처럼 모집단의 분산을 검증하거나 추정할 때 통계량 과 카이제곱 분포는 매우 유용하게 사용될 수 있다.
예제를 하나 더 살펴보자.
과일 음료수를 만드는 회사에서 무게 250g의 음료수를 만드는데,
음료수 무게의 표준 편차를 조사하고자 한다.
과거에 조사한 데이터에 따르면

라는 것이 알려져있다.
이에 회사에서는 25개의 음료수를 무작위로 추출하여 을 계산해봤다.
음료수의 무게가 정규 분포를 이루고 있다고 가정하고 다음 조건을 만족하는 b값을 구하여라.
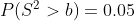
(풀이)

따라서,


즉,

만약 위 회사에서 24개의 표본을 추출하여 조사해본 결과
의 값이 3.03을 넘었다면 이것은 굉장히 예외적인 경우로서
원래 알고 있던 표준편차가 틀렸거나 조사가 잘못된 것이라고 볼 수 있다.
'통계 빠개기 > Statistics' 카테고리의 다른 글
| [Overview] 확률 분포 (0) | 2020.05.21 |
|---|---|
| [Distribution] 확률 분포 간 관계도 (0) | 2020.05.20 |
| [Distribution] Geometric, Negative Binomial의 정의, 기대값, 분산 (0) | 2020.05.20 |
| [Video] 이산 확률 분포_ 기하분포, 음이항분포, 초기하분포 (0) | 2020.05.20 |
| [이산 확률 분포] 베르누이, 이항, 포아송 분포 (0) | 2020.05.20 |